# Deep Learning Library: accel-brain-base.
`accel-brain-base` is a basic library of the Deep Learning for rapid development at low cost. This library makes it possible to design and implement deep learning, which must be configured as a complex system or a System of Systems, by combining a plurality of functionally differentiated modules such as a Restricted Boltzmann Machine(RBM), Deep Boltzmann Machines(DBMs), a Stacked-Auto-Encoder, an Encoder/Decoder based on Long Short-Term Memory(LSTM), and a Convolutional Auto-Encoder(CAE).
From the view points of functionally equivalents and structural expansions, this library also prototypes many variants such as energy-based models and Generative models. Typical examples are Generative Adversarial Networks(GANs) and Adversarial Auto-Encoders(AAEs). In addition, it provides deep reinforcement learning that applies the neural network described above as a function approximator.
See also ...
- [Automatic Summarization Library: pysummarization](https://github.com/accel-brain/accel-brain-code/tree/master/Automatic-Summarization)
* If you want to implement the Sequence-to-Sequence(Seq2Seq) model for the automatic summarization by using `accel-brain-base` to build the Encoder/Decoder controllers.
- [Reinforcement Learning Library: pyqlearning](https://github.com/accel-brain/accel-brain-code/tree/master/Reinforcement-Learning)
* If you want to implement the Deep Reinforcement Learning, especially for Deep Q-Network and Multi-agent Deep Q-Network by using `accel-brain-base` as a Function Approximator.
- [Generative Adversarial Networks Library: pygan](https://github.com/accel-brain/accel-brain-code/tree/master/Generative-Adversarial-Networks)
* If you want to implement Generative Adversarial Networks(GANs) and Adversarial Auto-Encoders(AAEs) by using `accel-brain-base` as components for Generative models based on the Statistical machine learning problems.
- [Algorithmic Composition or Automatic Composition Library: pycomposer](https://github.com/accel-brain/accel-brain-code/tree/master/Algorithmic-Composition)
* If you want to implement the Algorithmic Composer based on Generative Adversarial Networks(GANs) by using `accel-brain-base` as components for Generative models based on the Statistical machine learning problems.
## Installation
Install using pip:
```sh
pip install accel-brain-base
```
### Source code
The source code is currently hosted on GitHub.
- [accel-brain-code/Accel-Brain-Base](https://github.com/accel-brain/accel-brain-code/tree/master/Accel-Brain-Base)
### Python package index(PyPI)
Installers for the latest released version are available at the Python package index.
- [accel-brain-base : Python Package Index](https://pypi.python.org/pypi/accel-brain-base/)
### Dependencies
- [numpy](https://github.com/numpy/numpy): v1.13.3 or higher.
- [pandas](https://github.com/pandas-dev/pandas): v0.22.0 or higher.
- [mxnet](https://github.com/apache/incubator-mxnet) or [mxnet-cu*](https://mxnet.apache.org/api/python/docs/tutorials/getting-started/crash-course/6-use_gpus.html): latest.
#### For ML Ops.
In this library, almost all models inherit [HybridBlock](https://gluon.mxnet.io/chapter07_distributed-learning/hybridize.html) from [mxnet.gluon](https://mxnet.incubator.apache.org/api/python/docs/api/gluon/index.html). Functions for common ML Ops such as saving and loading parameters are provided by [HybridBlock](https://mxnet.apache.org/api/python/docs/api/gluon/hybrid_block.html).
**Note** that, however, we are using [HybridBlocks](https://gluon.mxnet.io/chapter07_distributed-learning/hybridize.html) in [mxnet.gluon](https://mxnet.incubator.apache.org/api/python/docs/api/gluon/index.html) at present but we will also implement functional equivalents that use TensorFlow and PyTorch in the future. There is no reason to stick to one library.
## Documentation
Full documentation is available on [https://code.accel-brain.com/Accel-Brain-Base/README.html](https://code.accel-brain.com/Accel-Brain-Base/README.html). This document contains information on functionally reusability, functional scalability and functional extensibility.
## Problem Setting: Deep Learning after the era of "Democratization of Artificial Intelligence(AI)".
How the Research and Development(R&D) on the subject of machine learning including deep learning, after the era of "Democratization of Artificial Intelligence(AI)", can become possible? Simply implementing the models and algorithms provided by standard machine learning libraries and applications like AutoML would reinvent the wheel. If you just copy and paste the demo code from the library and use it, your R&D would fall into dogmatically authoritarian development, or so-called the Hype driven development.
If you fall in love with the concept of "Democratization of AI," you may forget the reality that the R&D is under the influence of not only democracy but also capitalism. The R&D provides economic value when its R&D artifacts are distinguished from the models and algorithms realized by standard machine learning libraries and applications such as AutoML. In general terms, R&D must provide a differentiator to maximize the scarcity of its implementation artifacts.
On the other hand, it must be remembered that any R&D builds on the history of the social structure and the semantics of the concepts envisioned by previous studies. Many models and algorithms are variants derived not only from research but also from the relationship with business domains. It is impossible to assume differentiating factors without taking commonality and identity between society and its history.
Considering many variable parts, structural unions, and *functional equivalents* in the deep learning paradigm, which are variants derived not only from research but also from the relationship with business domains, from perspective of *commonality/variability analysis* in order to practice object-oriented design, this library provides abstract classes that define the skeleton of the deep Learning algorithm in an operation, deferring some steps in concrete variant algorithms such as the **Deep Boltzmann Machines**, **Stacked Auto-Encoder**, **Encoder/Decoder based on LSTM**, and **Convolutional Auto-Encoder** to client subclasses. The abstract classes and the interfaces in this library let subclasses redefine certain steps of the deep Learning algorithm without changing the algorithm's structure.
These abstract classes can also provide new original models and algorithms such as **Generative Adversarial Networks(GANs)**, **Deep Reinforcement Learning**, or **Neural network language model** by implementing the variable parts of the fluid elements of objects.
### Problem Solution: Deep Boltzmann Machines.
The function of this library is building and modeling Restricted Boltzmann Machine(RBM) and Deep Boltzmann Machine(DBM). The models are functionally equivalent to stacked auto-encoder. The basic function is the same as dimensions reduction or pre-learning for so-called transfer learning.
#### The structure of RBM.
According to graph theory, the structure of RBM corresponds to a complete bipartite graph which is a special kind of bipartite graph where every node in the visible layer is connected to every node in the hidden layer. Based on statistical mechanics and thermodynamics(Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. 1985), the state of this structure can be reflected by the energy function:
where  is a bias in visible layer,
is a bias in visible layer,  is a bias in hidden layer,
is a bias in hidden layer,  is an activity or a state in visible layer,
is an activity or a state in visible layer,  is an activity or a state in hidden layer, and
is an activity or a state in hidden layer, and  is a weight matrix in visible and hidden layer. The activities can be calculated as the below product, since the link of activations of visible layer and hidden layer are conditionally independent.
#### The learning equations of RBM.
Because of the rules of conditional independence, the learning equations of RBM can be introduced as simple form. The distribution of visible state
is a weight matrix in visible and hidden layer. The activities can be calculated as the below product, since the link of activations of visible layer and hidden layer are conditionally independent.
#### The learning equations of RBM.
Because of the rules of conditional independence, the learning equations of RBM can be introduced as simple form. The distribution of visible state  which is marginalized over the hidden state
which is marginalized over the hidden state  is as following:
where
is as following:
where 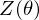 is a partition function in statistical mechanics or thermodynamics. Let
is a partition function in statistical mechanics or thermodynamics. Let  be set of observed data points, then
be set of observed data points, then  . Therefore the gradients on the parameter
. Therefore the gradients on the parameter  of the log-likelihood function are
where
of the log-likelihood function are
where 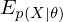 is an expected value for
is an expected value for  .
.  is a sigmoid function.
The learning equations of RBM are introduced by performing control so that those gradients can become zero.
#### Contrastive Divergence as an approximation method.
In relation to RBM, **Contrastive Divergence**(CD) is a method for approximation of the gradients of the log-likelihood(Hinton, G. E. 2002). The procedure of this method is similar to Markov Chain Monte Carlo method(MCMC). However, unlike MCMC, the visbile variables to be set first in visible layer is not randomly initialized but the observed data points in training dataset are set to the first visbile variables. And, like Gibbs sampler, drawing samples from hidden variables and visible variables is repeated `k` times. Empirically (and surprisingly), `k` is considered to be `1`.
#### The structure of DBM.
is a sigmoid function.
The learning equations of RBM are introduced by performing control so that those gradients can become zero.
#### Contrastive Divergence as an approximation method.
In relation to RBM, **Contrastive Divergence**(CD) is a method for approximation of the gradients of the log-likelihood(Hinton, G. E. 2002). The procedure of this method is similar to Markov Chain Monte Carlo method(MCMC). However, unlike MCMC, the visbile variables to be set first in visible layer is not randomly initialized but the observed data points in training dataset are set to the first visbile variables. And, like Gibbs sampler, drawing samples from hidden variables and visible variables is repeated `k` times. Empirically (and surprisingly), `k` is considered to be `1`.
#### The structure of DBM.
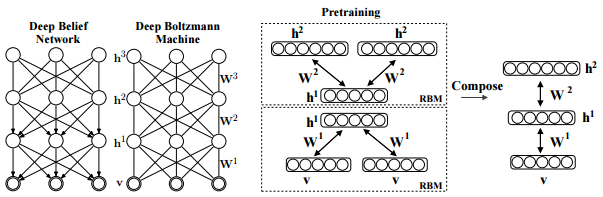
Salakhutdinov, R., Hinton, G. E. (2009). Deep boltzmann machines. In International conference on artificial intelligence and statistics (pp. 448-455). p451.
As is well known, DBM is composed of layers of RBMs stacked on top of each other(Salakhutdinov, R., & Hinton, G. E. 2009). This model is a structural expansion of Deep Belief Networks(DBN), which is known as one of the earliest models of Deep Learning(Le Roux, N., & Bengio, Y. 2008). Like RBM, DBN places nodes in layers. However, only the uppermost layer is composed of undirected edges, and the other consists of directed edges. DBN with `R` hidden layers is below probabilistic model:
where `r = 0` points to visible layer. Considerling simultaneous distribution in top two layer,
and conditional distributions in other layers are as follows:
The pre-learning of DBN engages in a procedure of recursive learning in layer-by-layer. However, as you can see from the difference of graph structure, DBM is slightly different from DBN in the form of pre-learning. For instance, if `r = 1`, the conditional distribution of visible layer is
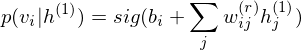
.

.

.
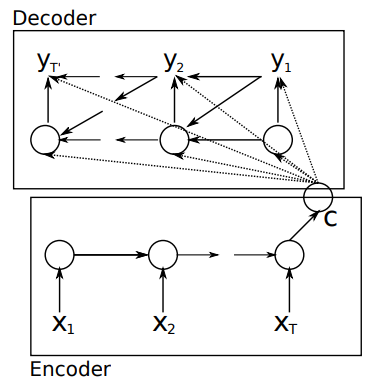
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078., p2.

Reconstructed image by Convolutional Auto-Encoder.
This library can draw a distinction between **Stacked Auto-Encoder** and **Convolutional Auto-Encoder**, and is able to design and implement respective models. **Stacked Auto-Encoder** ignores the 2 dimentional image structures. In many cases, the rank of observed tensors extracted from image dataset is more than 3. This is not only a problem when dealing with realistically sized inputs, but also introduces redundancy in the parameters, forcing each feature to be global. Like **Shape-BM**, **Convolutional Auto-Encoder** differs from **Stacked Auto-Encoder** as their weights are shared among all locations in the input, preserving spatial locality. Hence, the reconstructed image data is due to a linear combination of basic image patches based on the latent code.
In this library, **Convolutional Auto-Encoder** is also based on **Encoder/Decoder** scheme. The *encoder* is to the *decoder* what the *Convolution* is to the *Deconvolution*. The Deconvolution also called transposed convolutions "work by swapping the forward and backward passes of a convolution." (Dumoulin, V., & Visin, F. 2016, p20.)
In relation to the Representation Learning, like DBM, this model also can minimize the reconstruction errors. An example can be found in [demo/Convolutional-Auto-Encoder-for-Representation-Learning.ipynb](https://github.com/accel-brain/accel-brain-code/blob/master/Accel-Brain-Base/demo/Convolutional-Auto-Encoder-for-Representation-Learning.ipynb).
### Functionally equivalent: Convolutional Contractive Auto-Encoder.
This library also provides some functionally equivalents of the Convolutional Auto-Encoder. For instance, Convolutional Contractive Auto-Encoder(Contractive CAE) is a Convolutional Auto-Encoder based on the First-Order Contractive Auto-Encoder(Rifai, S., et al., 2011), which executes the representation learning by adding a penalty term to the classical reconstruction cost function. This penalty term corresponds to the Frobenius norm of the Jacobian matrix of the encoder activations with respect to the input and results in a localized space contraction which in turn yields robust features on the activation layer.
Analogically, the Contractive Convolutional Auto-Encoder calculates the penalty term. But it differs in that the operation of the deconvolution intervenes insted of inner product. The prototype is exemplified in [demo/Contractive-Convolutional-Auto-Encoder-for-Representation-Learning.ipynb](https://github.com/accel-brain/accel-brain-code/blob/master/Accel-Brain-Base/demo/Contractive-Convolutional-Auto-Encoder-for-Representation-Learning.ipynb).
## Issue: Structural extension from Auto-Encoders and Encoder/Decoders to energy-based models and Generative models.
Auto-Encoders, such as the Encoder/Decoder, the Convolutional Auto-Encoder, and the DBM have in common that these models are Stacked Auto-Encoders or the reconstruction models. On the other hand, the Auto-Encoders and the Encoder/Decoders are not statistical mechanical energy-based models unlike with RBM or DBM.
However, Auto-Encoders have traditionally been used to represent energy-based models. According to the statistical mechanical theory for energy-based models, Auto-Encoders constructed by neural networks can be associated with an energy landscape, akin to negative log-probability in a probabilistic model, which measures how well the Auto-Encoder can represent regions in the input space. The energy landscape has been commonly inferred heuristically, by using a training criterion that relates the Auto-Encoder to a probabilistic model such as a RBM. The energy function is identical to the free energy of the corresponding RBM, showing that Auto-Encoders and RBMs may be viewed as two different ways to derive training criteria for forming the same type of analytically defined energy landscape.
The view of the Auto-Encoder as a dynamical system allows us to understand how an energy function may be derived for the Auto-Encoder. This makes it possible to assign energies to Auto-Encoders with many different types of activation functions and outputs, and consider minimanization of reconstruction errors as energy minimanization(Kamyshanska, H., & Memisevic, R., 2014).
When trained with some regularization terms, the Auto-Encoders have the ability to learn an energy manifold without supervision or negative examples(Zhao, J., et al., 2016). This means that even when an energy-based Auto-Encoding model is trained to reconstruct a real sample, the model contributes to discovering the data manifold by itself.
This library provides energy-based Auto-Encoders such as Contractive Convolutional Auto-Encoder(Rifai, S., et al., 2011), Repelling Convolutional Auto-Encoder(Zhao, J., et al., 2016), Denoising Auto-Encoders(Bengio, Y., et al., 2013), and Ladder Networks(Valpola, H., 2015). But it is more usefull to redescribe the Auto-Encoders in the framework of Generative Adversarial Networks(GANs)(Goodfellow, I., et al., 2014) to make those models function as not only energy-based models but also Generative models. For instance, theory of an Adversarial Auto-Encoders(AAEs)(Makhzani, A., et al., 2015) and energy-based GANs(EBGANs)(Zhao, J., et al., 2016) enables us to turn Auto-Encoders into a Generative models which referes energy functions.
### Problem Solution: Generative Adversarial Networks(GANs).
The Generative Adversarial Networks(GANs) (Goodfellow et al., 2014) framework establishes a
min-max adversarial game between two neural networks – a generative model, `G`, and a discriminative
model, `D`. The discriminator model, `D(x)`, is a neural network that computes the probability that
a observed data point `x` in data space is a sample from the data distribution (positive samples) that we are trying to model, rather than a sample from our generative model (negative samples). Concurrently, the generator uses a function `G(z)` that maps samples `z` from the prior `p(z)` to the data space. `G(z)` is trained to maximally confuse the discriminator into believing that samples it generates come from the data distribution. The generator is trained by leveraging the gradient of `D(x)` w.r.t. `x`, and using that to modify its parameters.
### Problem Solution: *Conditional* GANs (or cGANs).
The *Conditional* GANs (or cGANs) is a simple extension of the basic GAN model which allows the model to condition on external information. This makes it possible to engage the learned generative model in different "modes" by providing it with different contextual information (Gauthier, J. 2014).
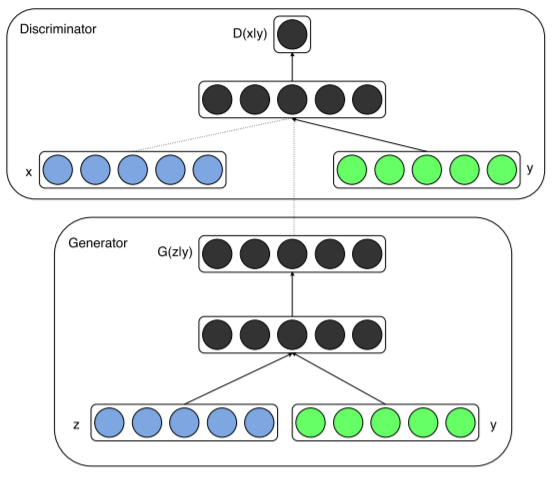
Mirza, M., & Osindero, S. (2014). Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784., p3.
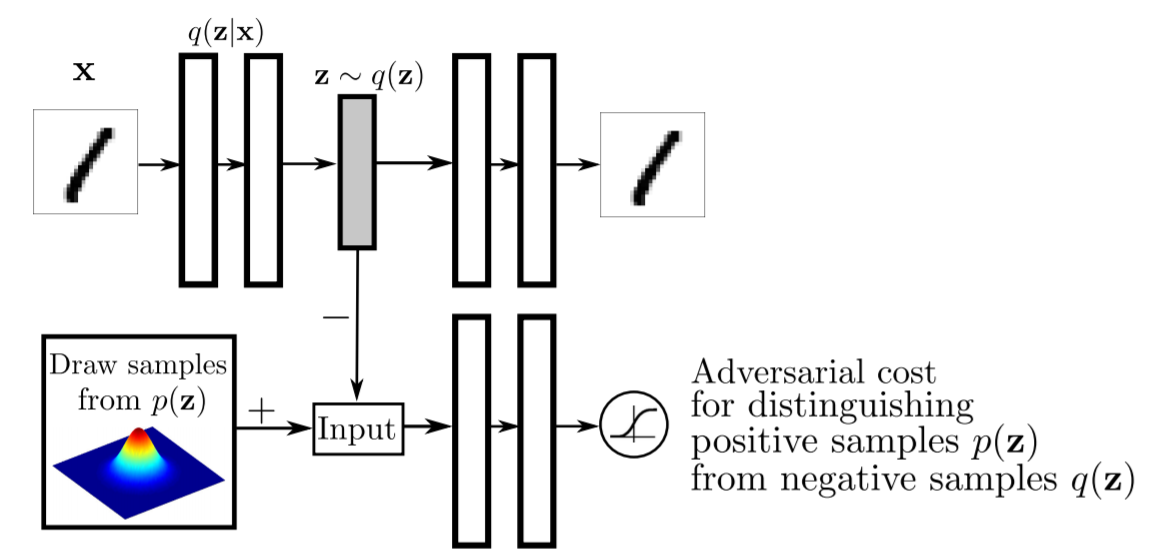
Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. (2015). Adversarial autoencoders. arXiv preprint arXiv:1511.05644., p2.
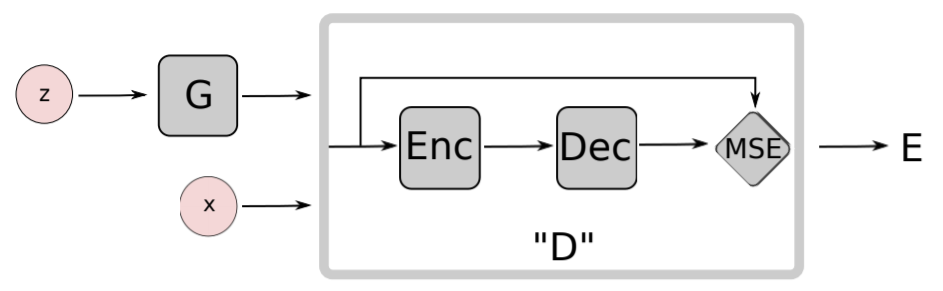
Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126., p4.
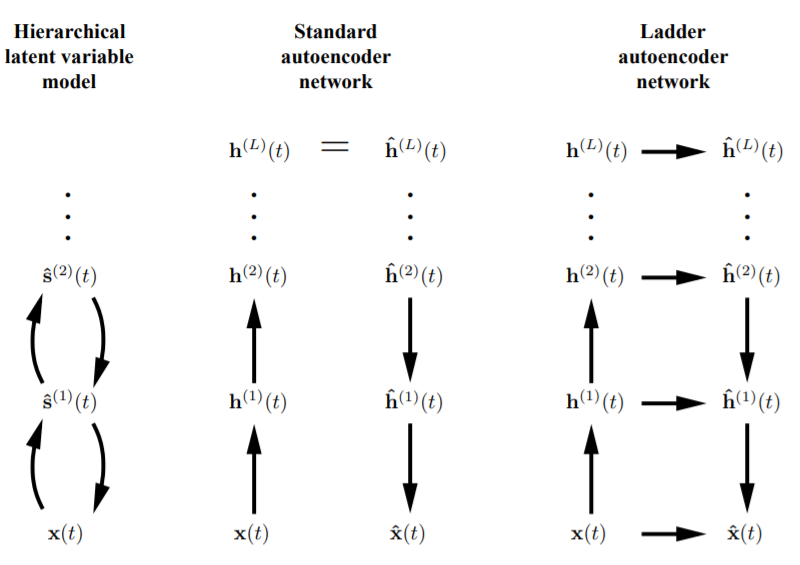
Valpola, H. (2015). From neural PCA to deep unsupervised learning. In Advances in independent component analysis and learning machines (pp. 143-171). Academic Press., p6.
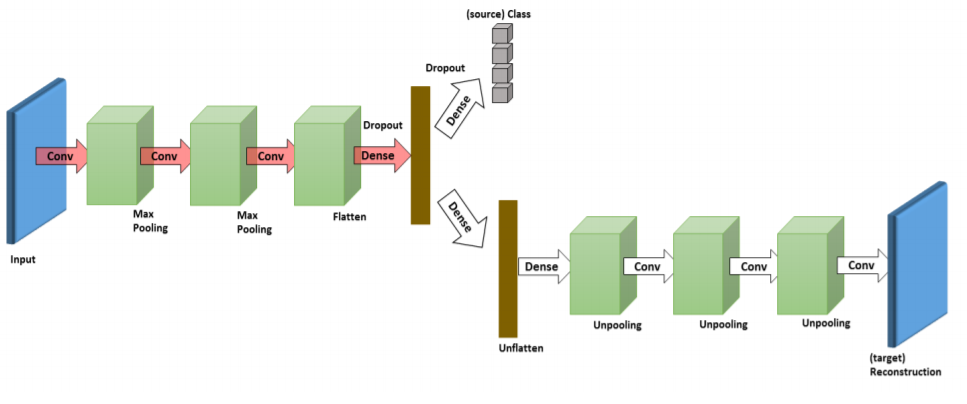
Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham., p5.
 , in a sequence of actions, observations and rewards. At each time-step the agent selects an action at from the set of possible actions,
, in a sequence of actions, observations and rewards. At each time-step the agent selects an action at from the set of possible actions,  . The state/action-value function is
. The state/action-value function is  .
The goal of the agent is to interact with the
.
The goal of the agent is to interact with the  by selecting actions in a way that maximises future rewards. We can make the standard assumption that future rewards are discounted by a factor of $\gamma$ per time-step, and define the future discounted return at time
by selecting actions in a way that maximises future rewards. We can make the standard assumption that future rewards are discounted by a factor of $\gamma$ per time-step, and define the future discounted return at time  as
as
 ,
where
,
where  is the time-step at which the agent will reach the goal. This library defines the optimal state/action-value function
is the time-step at which the agent will reach the goal. This library defines the optimal state/action-value function 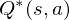 as the maximum expected return achievable by following any strategy, after seeing some state
as the maximum expected return achievable by following any strategy, after seeing some state  and then taking some action
and then taking some action  ,
,

,
where  is a policy mapping sequences to actions (or distributions over actions).
The optimal state/action-value function obeys an important identity known as the Bellman equation. This is based on the following *intuition*: if the optimal value
is a policy mapping sequences to actions (or distributions over actions).
The optimal state/action-value function obeys an important identity known as the Bellman equation. This is based on the following *intuition*: if the optimal value  of the sequence
of the sequence 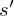 at the next time-step was known for all possible actions
at the next time-step was known for all possible actions  , then the optimal strategy is to select the action
, then the optimal strategy is to select the action  maximising the expected value of
maximising the expected value of

,

.
The basic idea behind many reinforcement learning algorithms is to estimate the state/action-value function, by using the Bellman equation as an iterative update,

.
Such *value iteration algorithms* converge to the optimal state/action-value function,  as
as  .
But increasing the complexity of states/actions is equivalent to increasing the number of combinations of states/actions. If the value function is continuous and granularities of states/actions are extremely fine, the combinatorial explosion will be encountered. In other words, this basic approach is totally impractical, because the state/action-value function is estimated separately for each sequence, without any **generalisation**. Instead, it is common to use a **function approximator** to estimate the state/action-value function,
So the Reduction of complexities is required.
### Problem Solution: Deep Q-Network
In this problem setting, the function of nerual network or deep learning is a function approximation with weights
.
But increasing the complexity of states/actions is equivalent to increasing the number of combinations of states/actions. If the value function is continuous and granularities of states/actions are extremely fine, the combinatorial explosion will be encountered. In other words, this basic approach is totally impractical, because the state/action-value function is estimated separately for each sequence, without any **generalisation**. Instead, it is common to use a **function approximator** to estimate the state/action-value function,
So the Reduction of complexities is required.
### Problem Solution: Deep Q-Network
In this problem setting, the function of nerual network or deep learning is a function approximation with weights  as a Q-Network. A Q-Network can be trained by minimising a loss functions
as a Q-Network. A Q-Network can be trained by minimising a loss functions  that changes at each iteration
that changes at each iteration  ,
where
is the target for iteration
,
where
is the target for iteration  and
and  is a so-called behaviour distribution. This is probability distribution over states and actions. The parameters from the previous iteration
is a so-called behaviour distribution. This is probability distribution over states and actions. The parameters from the previous iteration  are held fixed when optimising the loss function
are held fixed when optimising the loss function  . Differentiating the loss function with respect to the weights we arrive at the following gradient,
### Functional equivalent: MobileNet.
If you pay attention to the calculation speed, it is better to extend the CNN part that is the function approximation to MobileNet. As mentioned in [demo/MobileNet-v2-for-Image-Classification.ipynb](https://github.com/accel-brain/accel-brain-code/blob/master/Accel-Brain-Base/demo/MobileNet-v2-for-Image-Classification.ipynb), this library provides the MobileNet V2(Sandler, M., et al., 2018).
### Functional equivalent: LSTM.
It is not inevitable to functionally reuse CNN as a function approximator. In the above problem setting of generalisation and Combination explosion, for instance, Long Short-Term Memory(LSTM) networks, which is-a special Reccurent Neural Network(RNN) structure, and CNN as a function approximator are functionally equivalent. In the same problem setting, functional equivalents can be functionally replaced. Considering that the feature space of the rewards has the time-series nature, LSTM will be more useful.
## References
### Deep Boltzmann machines.
- Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive science, 9(1), 147-169.
- Boulanger-Lewandowski, N., Bengio, Y., & Vincent, P. (2012). Modeling temporal dependencies in high-dimensional sequences: Application to polyphonic music generation and transcription. arXiv preprint arXiv:1206.6392.
- Eslami, S. A., Heess, N., Williams, C. K., & Winn, J. (2014). The shape boltzmann machine: a strong model of object shape. International Journal of Computer Vision, 107(2), 155-176.
- Hinton, G. E. (2002). Training products of experts by minimizing contrastive divergence. Neural computation, 14(8), 1771-1800.
- Le Roux, N., & Bengio, Y. (2008). Representational power of restricted Boltzmann machines and deep belief networks. Neural computation, 20(6), 1631-1649.
- Lyu, Q., Wu, Z., Zhu, J., & Meng, H. (2015, June). Modelling High-Dimensional Sequences with LSTM-RTRBM: Application to Polyphonic Music Generation. In IJCAI (pp. 4138-4139).
- Lyu, Q., Wu, Z., & Zhu, J. (2015, October). Polyphonic music modelling with LSTM-RTRBM. In Proceedings of the 23rd ACM international conference on Multimedia (pp. 991-994). ACM.
- Salakhutdinov, R., & Hinton, G. E. (2009). Deep boltzmann machines. InInternational conference on artificial intelligence and statistics (pp. 448-455).
- Sutskever, I., Hinton, G. E., & Taylor, G. W. (2009). The recurrent temporal restricted boltzmann machine. In Advances in Neural Information Processing Systems (pp. 1601-1608).
### Auto-Encoders.
- Baccouche, M., Mamalet, F., Wolf, C., Garcia, C., & Baskurt, A. (2012, September). Spatio-Temporal Convolutional Sparse Auto-Encoder for Sequence Classification. In BMVC (pp. 1-12).
- Bengio, Y., Yao, L., Alain, G., & Vincent, P. (2013). Generalized denoising auto-encoders as generative models. In Advances in neural information processing systems (pp. 899-907).
- Chong, Y. S., & Tay, Y. H. (2017, June). Abnormal event detection in videos using spatiotemporal autoencoder. In International Symposium on Neural Networks (pp. 189-196). Springer, Cham.
- Masci, J., Meier, U., Cireşan, D., & Schmidhuber, J. (2011, June). Stacked convolutional auto-encoders for hierarchical feature extraction. In International Conference on Artificial Neural Networks (pp. 52-59). Springer, Berlin, Heidelberg.
- Patraucean, V., Handa, A., & Cipolla, R. (2015). Spatio-temporal video autoencoder with differentiable memory. arXiv preprint arXiv:1511.06309.
- Rifai, S., Vincent, P., Muller, X., Glorot, X., & Bengio, Y. (2011, June). Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the 28th International Conference on International Conference on Machine Learning (pp. 833-840). Omnipress.
- Rifai, S., Mesnil, G., Vincent, P., Muller, X., Bengio, Y., Dauphin, Y., & Glorot, X. (2011, September). Higher order contractive auto-encoder. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (pp. 645-660). Springer, Berlin, Heidelberg.
- Seung, H. S. (1998). Learning continuous attractors in recurrent networks. In Advances in neural information processing systems (pp. 654-660).
- Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126.
### Encoder/Decoder schemes with an Attention mechanism.
- Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
- Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., & Shroff, G. (2016). LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv preprint arXiv:1607.00148.
- Xingjian, S. H. I., Chen, Z., Wang, H., Yeung, D. Y., Wong, W. K., & Woo, W. C. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems (pp. 802-810).
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in Neural Information Processing Systems (pp. 5998-6008).
### Generative Adversarial Networks(GANs).
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... & Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems (pp. 2672-2680).
- Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. (2015). Adversarial autoencoders. arXiv preprint arXiv:1511.05644.
- Mirza, M., & Osindero, S. (2014). Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784.
- Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126.
### Unsupervised / Supervised pre-training
- Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2007). Greedy layer-wise training of deep networks. In Advances in neural information processing systems (pp. 153-160).
- Erhan, D., Bengio, Y., Courville, A., Manzagol, P. A., Vincent, P., & Bengio, S. (2010). Why does unsupervised pre-training help deep learning?. Journal of Machine Learning Research, 11(Feb), 625-660.
### Semi-supervised learning.
- Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham.
- Rasmus, A., Berglund, M., Honkala, M., Valpola, H., & Raiko, T. (2015). Semi-supervised learning with ladder networks. In Advances in neural information processing systems (pp. 3546-3554).
- Valpola, H. (2015). From neural PCA to deep unsupervised learning. In Advances in Independent Component Analysis and Learning Machines (pp. 143-171). Academic Press.
### Deep Reinforcement Learning.
- Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
- Egorov, M. (2016). Multi-agent deep reinforcement learning.
- Gupta, J. K., Egorov, M., & Kochenderfer, M. (2017, May). Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems (pp. 66-83). Springer, Cham.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., & Shroff, G. (2016). LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv preprint arXiv:1607.00148.
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
- Sainath, T. N., Vinyals, O., Senior, A., & Sak, H. (2015, April). Convolutional, long short-term memory, fully connected deep neural networks. In Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on (pp. 4580-4584). IEEE.
- Xingjian, S. H. I., Chen, Z., Wang, H., Yeung, D. Y., Wong, W. K., & Woo, W. C. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems (pp. 802-810).
- Zaremba, W., Sutskever, I., & Vinyals, O. (2014). Recurrent neural network regularization. arXiv preprint arXiv:1409.2329.
### Optimizations.
- Bengio, Y., Boulanger-Lewandowski, N., & Pascanu, R. (2013, May). Advances in optimizing recurrent networks. In 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (pp. 8624-8628). IEEE.
- Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul), 2121-2159.
- Dozat, T. (2016). Incorporating nesterov momentum into adam., Workshop track - ICLR 2016.
- Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
### Algorithms, Arithmetic, Regularizations, and Representations learning.
- Dumoulin, V., & Visin, F. (2016). A guide to convolution arithmetic for deep learning. arXiv preprint arXiv:1603.07285.
- Erhan, D., Courville, A., & Bengio, Y. (2010). Understanding representations learned in deep architectures. Department dInformatique et Recherche Operationnelle, University of Montreal, QC, Canada, Tech. Rep, 1355, 1.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
- Ioffe, S., & Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167.
- Kamyshanska, H., & Memisevic, R. (2014). The potential energy of an autoencoder. IEEE transactions on pattern analysis and machine intelligence, 37(6), 1261-1273.
- Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., & Chen, L. C. (2018). Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4510-4520).
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929-1958.
- Zaremba, W., Sutskever, I., & Vinyals, O. (2014). Recurrent neural network regularization. arXiv preprint arXiv:1409.2329.
## Author
- accel-brain
## Author URI
- https://accel-brain.co.jp/
- https://accel-brain.com/
## License
- GNU General Public License v2.0
. Differentiating the loss function with respect to the weights we arrive at the following gradient,
### Functional equivalent: MobileNet.
If you pay attention to the calculation speed, it is better to extend the CNN part that is the function approximation to MobileNet. As mentioned in [demo/MobileNet-v2-for-Image-Classification.ipynb](https://github.com/accel-brain/accel-brain-code/blob/master/Accel-Brain-Base/demo/MobileNet-v2-for-Image-Classification.ipynb), this library provides the MobileNet V2(Sandler, M., et al., 2018).
### Functional equivalent: LSTM.
It is not inevitable to functionally reuse CNN as a function approximator. In the above problem setting of generalisation and Combination explosion, for instance, Long Short-Term Memory(LSTM) networks, which is-a special Reccurent Neural Network(RNN) structure, and CNN as a function approximator are functionally equivalent. In the same problem setting, functional equivalents can be functionally replaced. Considering that the feature space of the rewards has the time-series nature, LSTM will be more useful.
## References
### Deep Boltzmann machines.
- Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive science, 9(1), 147-169.
- Boulanger-Lewandowski, N., Bengio, Y., & Vincent, P. (2012). Modeling temporal dependencies in high-dimensional sequences: Application to polyphonic music generation and transcription. arXiv preprint arXiv:1206.6392.
- Eslami, S. A., Heess, N., Williams, C. K., & Winn, J. (2014). The shape boltzmann machine: a strong model of object shape. International Journal of Computer Vision, 107(2), 155-176.
- Hinton, G. E. (2002). Training products of experts by minimizing contrastive divergence. Neural computation, 14(8), 1771-1800.
- Le Roux, N., & Bengio, Y. (2008). Representational power of restricted Boltzmann machines and deep belief networks. Neural computation, 20(6), 1631-1649.
- Lyu, Q., Wu, Z., Zhu, J., & Meng, H. (2015, June). Modelling High-Dimensional Sequences with LSTM-RTRBM: Application to Polyphonic Music Generation. In IJCAI (pp. 4138-4139).
- Lyu, Q., Wu, Z., & Zhu, J. (2015, October). Polyphonic music modelling with LSTM-RTRBM. In Proceedings of the 23rd ACM international conference on Multimedia (pp. 991-994). ACM.
- Salakhutdinov, R., & Hinton, G. E. (2009). Deep boltzmann machines. InInternational conference on artificial intelligence and statistics (pp. 448-455).
- Sutskever, I., Hinton, G. E., & Taylor, G. W. (2009). The recurrent temporal restricted boltzmann machine. In Advances in Neural Information Processing Systems (pp. 1601-1608).
### Auto-Encoders.
- Baccouche, M., Mamalet, F., Wolf, C., Garcia, C., & Baskurt, A. (2012, September). Spatio-Temporal Convolutional Sparse Auto-Encoder for Sequence Classification. In BMVC (pp. 1-12).
- Bengio, Y., Yao, L., Alain, G., & Vincent, P. (2013). Generalized denoising auto-encoders as generative models. In Advances in neural information processing systems (pp. 899-907).
- Chong, Y. S., & Tay, Y. H. (2017, June). Abnormal event detection in videos using spatiotemporal autoencoder. In International Symposium on Neural Networks (pp. 189-196). Springer, Cham.
- Masci, J., Meier, U., Cireşan, D., & Schmidhuber, J. (2011, June). Stacked convolutional auto-encoders for hierarchical feature extraction. In International Conference on Artificial Neural Networks (pp. 52-59). Springer, Berlin, Heidelberg.
- Patraucean, V., Handa, A., & Cipolla, R. (2015). Spatio-temporal video autoencoder with differentiable memory. arXiv preprint arXiv:1511.06309.
- Rifai, S., Vincent, P., Muller, X., Glorot, X., & Bengio, Y. (2011, June). Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the 28th International Conference on International Conference on Machine Learning (pp. 833-840). Omnipress.
- Rifai, S., Mesnil, G., Vincent, P., Muller, X., Bengio, Y., Dauphin, Y., & Glorot, X. (2011, September). Higher order contractive auto-encoder. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (pp. 645-660). Springer, Berlin, Heidelberg.
- Seung, H. S. (1998). Learning continuous attractors in recurrent networks. In Advances in neural information processing systems (pp. 654-660).
- Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126.
### Encoder/Decoder schemes with an Attention mechanism.
- Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
- Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., & Shroff, G. (2016). LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv preprint arXiv:1607.00148.
- Xingjian, S. H. I., Chen, Z., Wang, H., Yeung, D. Y., Wong, W. K., & Woo, W. C. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems (pp. 802-810).
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in Neural Information Processing Systems (pp. 5998-6008).
### Generative Adversarial Networks(GANs).
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... & Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems (pp. 2672-2680).
- Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. (2015). Adversarial autoencoders. arXiv preprint arXiv:1511.05644.
- Mirza, M., & Osindero, S. (2014). Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784.
- Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126.
### Unsupervised / Supervised pre-training
- Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2007). Greedy layer-wise training of deep networks. In Advances in neural information processing systems (pp. 153-160).
- Erhan, D., Bengio, Y., Courville, A., Manzagol, P. A., Vincent, P., & Bengio, S. (2010). Why does unsupervised pre-training help deep learning?. Journal of Machine Learning Research, 11(Feb), 625-660.
### Semi-supervised learning.
- Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham.
- Rasmus, A., Berglund, M., Honkala, M., Valpola, H., & Raiko, T. (2015). Semi-supervised learning with ladder networks. In Advances in neural information processing systems (pp. 3546-3554).
- Valpola, H. (2015). From neural PCA to deep unsupervised learning. In Advances in Independent Component Analysis and Learning Machines (pp. 143-171). Academic Press.
### Deep Reinforcement Learning.
- Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
- Egorov, M. (2016). Multi-agent deep reinforcement learning.
- Gupta, J. K., Egorov, M., & Kochenderfer, M. (2017, May). Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems (pp. 66-83). Springer, Cham.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., & Shroff, G. (2016). LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv preprint arXiv:1607.00148.
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
- Sainath, T. N., Vinyals, O., Senior, A., & Sak, H. (2015, April). Convolutional, long short-term memory, fully connected deep neural networks. In Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on (pp. 4580-4584). IEEE.
- Xingjian, S. H. I., Chen, Z., Wang, H., Yeung, D. Y., Wong, W. K., & Woo, W. C. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems (pp. 802-810).
- Zaremba, W., Sutskever, I., & Vinyals, O. (2014). Recurrent neural network regularization. arXiv preprint arXiv:1409.2329.
### Optimizations.
- Bengio, Y., Boulanger-Lewandowski, N., & Pascanu, R. (2013, May). Advances in optimizing recurrent networks. In 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (pp. 8624-8628). IEEE.
- Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul), 2121-2159.
- Dozat, T. (2016). Incorporating nesterov momentum into adam., Workshop track - ICLR 2016.
- Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
### Algorithms, Arithmetic, Regularizations, and Representations learning.
- Dumoulin, V., & Visin, F. (2016). A guide to convolution arithmetic for deep learning. arXiv preprint arXiv:1603.07285.
- Erhan, D., Courville, A., & Bengio, Y. (2010). Understanding representations learned in deep architectures. Department dInformatique et Recherche Operationnelle, University of Montreal, QC, Canada, Tech. Rep, 1355, 1.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
- Ioffe, S., & Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167.
- Kamyshanska, H., & Memisevic, R. (2014). The potential energy of an autoencoder. IEEE transactions on pattern analysis and machine intelligence, 37(6), 1261-1273.
- Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., & Chen, L. C. (2018). Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4510-4520).
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929-1958.
- Zaremba, W., Sutskever, I., & Vinyals, O. (2014). Recurrent neural network regularization. arXiv preprint arXiv:1409.2329.
## Author
- accel-brain
## Author URI
- https://accel-brain.co.jp/
- https://accel-brain.com/
## License
- GNU General Public License v2.0


 is a bias in visible layer,
is a bias in visible layer,  is a bias in hidden layer,
is a bias in hidden layer,  is an activity or a state in visible layer,
is an activity or a state in visible layer,  is an activity or a state in hidden layer, and
is an activity or a state in hidden layer, and  is a weight matrix in visible and hidden layer. The activities can be calculated as the below product, since the link of activations of visible layer and hidden layer are conditionally independent.
is a weight matrix in visible and hidden layer. The activities can be calculated as the below product, since the link of activations of visible layer and hidden layer are conditionally independent.


 which is marginalized over the hidden state
which is marginalized over the hidden state  is as following:
is as following:

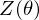 is a partition function in statistical mechanics or thermodynamics. Let
is a partition function in statistical mechanics or thermodynamics. Let  be set of observed data points, then
be set of observed data points, then  . Therefore the gradients on the parameter
. Therefore the gradients on the parameter  of the log-likelihood function are
of the log-likelihood function are
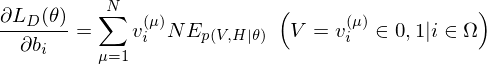


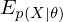 is an expected value for
is an expected value for  .
.  is a sigmoid function.
The learning equations of RBM are introduced by performing control so that those gradients can become zero.
is a sigmoid function.
The learning equations of RBM are introduced by performing control so that those gradients can become zero.


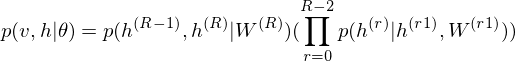


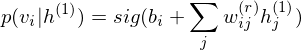 .
.
 .
. .
.







 , in a sequence of actions, observations and rewards. At each time-step the agent selects an action at from the set of possible actions,
, in a sequence of actions, observations and rewards. At each time-step the agent selects an action at from the set of possible actions,  . The state/action-value function is
. The state/action-value function is  .
The goal of the agent is to interact with the
.
The goal of the agent is to interact with the  by selecting actions in a way that maximises future rewards. We can make the standard assumption that future rewards are discounted by a factor of $\gamma$ per time-step, and define the future discounted return at time
by selecting actions in a way that maximises future rewards. We can make the standard assumption that future rewards are discounted by a factor of $\gamma$ per time-step, and define the future discounted return at time  as
as
 ,
where
,
where  is the time-step at which the agent will reach the goal. This library defines the optimal state/action-value function
is the time-step at which the agent will reach the goal. This library defines the optimal state/action-value function 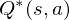 as the maximum expected return achievable by following any strategy, after seeing some state
as the maximum expected return achievable by following any strategy, after seeing some state  and then taking some action
and then taking some action  ,
,
 ,
,
 is a policy mapping sequences to actions (or distributions over actions).
The optimal state/action-value function obeys an important identity known as the Bellman equation. This is based on the following *intuition*: if the optimal value
is a policy mapping sequences to actions (or distributions over actions).
The optimal state/action-value function obeys an important identity known as the Bellman equation. This is based on the following *intuition*: if the optimal value  of the sequence
of the sequence 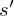 at the next time-step was known for all possible actions
at the next time-step was known for all possible actions  , then the optimal strategy is to select the action
, then the optimal strategy is to select the action  maximising the expected value of
maximising the expected value of
 ,
,
 .
.
 .
.
 as
as  .
But increasing the complexity of states/actions is equivalent to increasing the number of combinations of states/actions. If the value function is continuous and granularities of states/actions are extremely fine, the combinatorial explosion will be encountered. In other words, this basic approach is totally impractical, because the state/action-value function is estimated separately for each sequence, without any **generalisation**. Instead, it is common to use a **function approximator** to estimate the state/action-value function,
.
But increasing the complexity of states/actions is equivalent to increasing the number of combinations of states/actions. If the value function is continuous and granularities of states/actions are extremely fine, the combinatorial explosion will be encountered. In other words, this basic approach is totally impractical, because the state/action-value function is estimated separately for each sequence, without any **generalisation**. Instead, it is common to use a **function approximator** to estimate the state/action-value function,
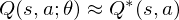
 as a Q-Network. A Q-Network can be trained by minimising a loss functions
as a Q-Network. A Q-Network can be trained by minimising a loss functions  that changes at each iteration
that changes at each iteration  ,
,


 and
and  is a so-called behaviour distribution. This is probability distribution over states and actions. The parameters from the previous iteration
is a so-called behaviour distribution. This is probability distribution over states and actions. The parameters from the previous iteration  are held fixed when optimising the loss function
are held fixed when optimising the loss function  . Differentiating the loss function with respect to the weights we arrive at the following gradient,
. Differentiating the loss function with respect to the weights we arrive at the following gradient,
